|
|
More Thermodynamics | ||
|
|
|
|
I pretend that I have a material that is a perfect insulator of heat. I make a cylinder and a piston of that material. One end of the cylinder is a disk, of the same material, that has two holes, through which passes a pipe that is shaped like a U . This is arranged so that a stream of water can run through the pipe. I let hot water flow in the pipe. The air in the cylinder expands, pushing the piston before it. Then I shut off the hot water. I let cold water flow in the pipe. The air in the cylinder contracts. The pressure of the outside air pushes the piston against the contracting inside air. If I assume that the piston is massless and frictionless, the heat that the engine receives from the pipe and the heat that the engine returns to the pipe are equal. The only difference is that the heat goes into the cylinder from a higher temperature source and goes out of the cylinder into a low temperature sink. If I attach a driving rod to the piston, and transfer energy to a machine of any kind, the cylinder must take in more heat to make the air inside expand against resistance. The engine gives the same amount of heat to the sink, with or without the driving rod. When the engine idles, the heat coming in is equal to the heat going out. When the engine drives a machine, the heat in is greater than the heat out. The difference in energy between heat in and heat out is the energy that drives the machine. Every machine has friction, so the work output of the machine is less than the energy supplied by the engine, which is equal to heat in minus heat out. If I disregard friction, there is still one problem. The energy that is supplied as heat-in is separated into heat-out and work. The work is less than the energy of the heat that is supplied, by the amount of heat out. The heat out is waste. Heat moves only in the direction that goes from a place of higher temperature to a place of lower temperature. In order to restore the heat from the place of lower temperature to a place of higher temperature, work must be done. Instead of pumping the heat back from the cold water to the hot water, I would use the more practical tactic of turning on the oil burner periodically to keep the hot water at an even temperature. The source of the energy for the machine is the flame of the oil burner. I do some accounting and find that the energy of the output of the machine is less than the energy of the fuel oil-oxygen reaction. Every engine does less useful work than the amount of energy that makes the engine run. An internal combustion engine does not receive heat from the outside. Energy to push a piston comes directly from the energy of the reaction of gasoline with oxygen. The energy is in the form of the kinetic energy of the molecules, partly translational, partly vibrational. The molecules strike the piston hard and often. That transfers kinetic energy to the piston, and reduces the kinetic energy of the gas molecules. Once the piston moves out to its limit, the action would stop, except that a valve opens to let the gases escape. Much heat escapes with the exhaust gases. The loss of energy in the exhaust is unavoidable. I use the example of the engine to repreent all processes. Any chemical reaction causes a local expansion or contaction of the air. Expanding air does work on the surroundings by pushing back the atmosphere. Air that is contracting has work done on it by the atmosphere. The chemical reaction in a battery transports electrons in a conductor. That is another example of doing work. If I move the books from the lower shelf to a higher shelf, I do work that is easily measured and calculated. The weight of the books and the distance between shelves, with a little algebra, tell us how much work was done. It is not that easy to measure the energy I had to expend in the task, but I am certain that it exceeded the figure for the work. I have two thermos bottles. One contains air at 360K, and the other contains air at 270K. I invert one bottle over the other, mouth to mouth. It does not matter which is on top. I leave the bottles that way for one hour. Now they have equal temperatures, approximately 315K. Heat goes from the place of higher temperature to the place of lower temperature until the temperature is uniform. By interacting with each other, molecules transfer energy. By interacting a billion times a second, each molecule has the same average kinetic energy of translation as all the other molecules. (translation is the motion of the molecule as a whole, not the vibration of its parts) When contact is made whereby heat can be transferred, it transfers in such a way as to result in the most probable arrangement. For instance it is more probable for the heat to be evenly distributed than it is for the heat to be divided between a hot region and a cold region. The tendency toward states of higher probability is called entropy. Entropy is entirely in the eye of the beholder. Probability is only a mental construct, and entropy describes probability quantitatively. I prefer to look for the mechanism in all things. Entropy is not a mechanism. I have already explained the transfer of heat in one direction in terms of molecular interactions. I shall now explain diffusion. A drop of ink in a glass of water slowly spreads in all directions, until it is evenly distributed throughout the glass of water. A drop of ammonia water on the table loses its ammonia molecules to the air. The odor of ammonia can be detected in all parts of the room in a few minutes. After an hour the distribution of ammonia in the room is uniform. During the process of diffusion, I concentrate on two adjacent spaces. Each space is a cubic centimeter. Space b contains a thousand ammonia molecules mixed with the air. Space c contains a hundred ammonia molecules mixed with the air. In any instant 1% of the molecules are crossing over to the adjacent space. That includes 10 ammonia molecules from space b and 1 ammonia molecule from space c. The distribution is altered after this exchange. The ratio becomes 991 to 109. With each exchange, the ratio gets closer to 550 to 550. Inevitably the distribution becomes even. A tank of compressed air is less probable than the same air distributed in the atmosphere. At the first opportunity, the air escapes. Suppose a small valve is opened, At the opening, there are more molecules per square centimeter on the inside than on the outside. A few molecules enter, but many more leave. If I were inclined to think in terms of entropy, I would say that when a gas that is confined to 1 cm3 is allowed to expand to 2 cm3, its entropy doubles. Helium is a gas at 10 K. I would assume that helium at 20 K has twice the entropy of helium at 10 K. In going from 90 K to 100 K, helium increases its entropy by 10/90. In going from 100 K to 110 K, helium increases its entropy by 10/100. If the entropy of 2 x 1010 molecules of helium at 100 K is S, the entropy of 1010 molecules of helium at 110 K is: (1/2)(110/100)(S). The 1/2 is there because 1010 molecules are half of 2 x 1010 molecules. S = 100/100 S, and an increase of 10/100 S makes a total of 110/100 S for 2 x 1010 molecules. The entropy of 1010 molecules of helium at 90 K is: (1/2)(90-10)/(90)(S) = 4/9 S Compared with: (1/2)(110/100)(S) = 55/100 S I mix the 1010 helium molecules at 110 K with the helium molecules at 90 K. I get 2 x 1010 molecules with an entropy of S. For 1010 molecules there is a loss of entropy of: (55/100)(S) - (1/2)(S) = 5/100 S For the other 1010 molecules , there is a gain in entropy of : (1/2)(S) - (40/90)(S) = 5/90 S I subtract the loss from the gain, and find that there is a net gain in the entropy for the 2 x 1010 molecules of: 5/90 S - 5/100 S = 5/900 S These are not the actual equations and figures. They are suitable simplifications designed to permit concentration on the central ideas, rather than on the mathematical details. The change in entropy is different at different tmperatures, and it is different for different substances. However, the principles are the same for all substances and all processes. Water at 373 K absorbs heat from a source at 374 K. The water continues to have the same temperature of 373 K, but it loses some of its molecules to the atmosphere. (at standard atmospheric pressure and temperature) The part that is liquid does not gain or lose entropy. The part that becomes steam is not at a higher temperature than 373 K, but it has a higher entropy, because the molecules are separated from each other. Disorder and dissociation are more probable than order and aggregation. A look at the mechanism, however, reveals that the water molecules that leave the water, have higher individual temperature, at the instant of leaving, than the average water molecule. By the time the departing water molecules have done their work of pushing back the atmosphere, they are at average temperature. The gain in entropy is very large. It is 1.8 x 10-15 erg per molecule. This should guarantee that water should only boil, and never condense. The point is that as the H2O gains entropy in changing from an orderly liquid to a disorderly gas, the surrounding air is banished from a volume it once occupied. That is improbable to the same degree that the evaporation of water is probable. The total entropy gained by the steam as it boils, is equal to the total entropy lost by the atmosphere as it loses volume. Let the temperature of the heater be reduced to 372 K. Boiling stops. More H2O molecules return to the liquid than leave. The surrounding air pushes the steam back toward the surface of the water, transferring energy to the H2O, and receiving entropy from the H2O molecules. This is a reversible process in the same sense as the reversibility of a massless piston in an insulated cylinder. Reversible processes and reversible engines are all imaginary. This cycle of boiling and condensing contains a slight deception. I did not take into account the difference in temperature between the heater and the water. For boiling, the heater was 374 K. For condensing, the heater was at 372 K. In order for real water to boil, the steam must gain more entropy than the atmosphere loses. In order for real steam to condense, the atmosphere must gain more entropy than the steam loses. Instead of giving all the entropy to the atmosphere directly, this system passed heat to the heater, because of the temperature difference during the condensing phase. During the boling phase, the fact that the heater was at a higher temperature than the water meant that several water molecules departed with more energy than necessary. The excess temperature and entropy was passed on to the atmosphere. It did not return during the condensation. The accounting for a chemical reaction is usually done at room temperature. The bond strengths at 298 K of the reactants and the products are compared. In nearly every reaction that goes in the right direction, the entropy decreases. Weak bonds are replaced by strong bonds. Strong bonds hold things closer together and in less disorder. This leaves out the contact between the reaction and the surroundings. In order for strong bonds to form, energy must be transferred to the environment. During the course of the reaction, the temperature of the reacting material rises. Heat is transferred from the reaction at high temperature, to the environment, which has a lower temperature. The change in entropy is greater at lower temperatures than at higher temperatures. As a consequence, the environment gains more entropy than the reacting materials lose.
Entropy 101
Mercury is a liquid at room temperature. Mercury boils at 630 K. The reaction of mercury with oxygen goes in the right direction. but the energy of the reaction is small. At room temperature, nothing happens. At about 600 K, oxygen unites with mercury. At about 1000 K, the oxygen and the mercury separate. The reaction that separates mercury from oxygen goes in the wrong direction. It proceeds because the energy of vibration between the oxygen nucleus and the mercury nucleus at that temperature is geater than the bond energy. It can also be shown that the entropy that the environment loses in transferring energy to the reacting materials is less than the entropy gained by the reacting materials in becoming separated from each other. There are a few other instances of reactions that go in the wrong direction. However there are no exceptions to the rule that only those reactions are permitted that increase the quantity of entropy in the universe. If I want to reverse a reaction, I can link it with a right direction reaction. For the combined reaction, the entropy of the universe increases. The word gets around that there is a tendency in the universe to arrive at a uniform temperature and a maximum entropy throughout. At that point, nothing else can happen. The fallacy is the extrapolation of our limited experience to a vast, and probably unlimited universe. There are places in the universe that have temperatures and pressures greater than we can comprehend. We just don't know enough to make rules for the universe. I have calculated the total entropies at different temperatures, using a formula for the rate of change of entropy for a process in which heat is transferred from a place of higher temperature to a place of lower temperature. (Fig. 1)
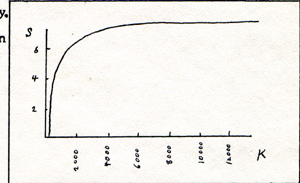
S is the symbol for entropy. Entropy increases rapidly between zero and ten K. It increases perceptibly between 100 K and 5000 K. At 12000 K, it increases less than 1% per 1000 degrees change in temperature. Evidently, entropy is of interest mainly at low temperatures. Entropy is of no great significance in much of the universe, where temperatures are often in the millions of degrees. Entropy is used in chemistry for calculating which way a reaction is likely to go, and in finding the equilibrium point. A reaction seems to stop. Very often the reaction that seems to have stopped, is going on in both directions at once. If the forward reaction and the reverse reaction are occuring at the same rate, there seems to be no reaction at all. This is called equilibrium. The ratio is called the equilibrium constant. The chemist finds the entropy in a chart in a reference book, substitutes the figure in an equation, and calculates the equilibrium ratio. The chemists who had the job of preparing the chart, calculated the entropy from the equilibrium ratio that they found in an experiment. From the manner in which the entropy fits into the calculations, I would say that entropy is a catchall for the factors in a chemical reaction, that tend to drive the reaction in the reverse direction. Some of these factors are high temperature, low density, fragmentation, and disorder.
next page