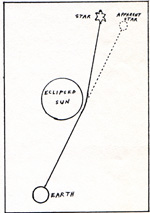
The velocity of light is measured for light whose sender and receiver are not moving relative to each other. The result is always the same for instruments of equal precision and accuracy. The velocity of light is not measured for moving senders. There is a postulate that the velocity of light is the same for all receivers and senders, if their relative motion is not accelerated, and if there is no strong gravitational field. A postulate is an assumption. An assumption is never proved. It is understood that the path of a ray of light is bent in a strong gravitational field. During a total eclipse of the sun, the sky is like a night sky. The stars are visible. A star whose light passes close to the sun appears to be shifted from its expected position, because the path of the light is curved. (Fig. 1) Click on image to enlarge. Use Back to return.

The diagram is greatly exaggerated. The observed shift is very small. Another demonstration that the force of gravity accelerates or decelerates photons, is the shift in frequency of gamma ray photons. Photons are emitted from the bottom of a tower, and received at the top of the tower. Then the sender and receiver reverse places. The photons are emitted from the top of the tower, and received at the bottom. It is observed that the photons which are received at the bottom have a higher frequency than the photons which are received at the top. This shows that photons accelerate in a gravitational field, even when the sender and receiver are stationary. Standard science has its own picture of the hydrogen atom. The important force between the proton and the electron is the electrostatic attraction between a positive and a negative charge. There is a lesser force, a magnetic force due to spin. There is also a negligible force of gravitation. The electron and the proton don't rush toward each other and stick together, because there is no way for the electron to lose the last of its energy. The electron can lose energy until it gets down to energy level number 1. It cannot lose the rest of its energy. One reason why the electron can't lose the lowest energy is the uncertainty principle, which states that an electron cannot have a definite position and a definite momentum at the same time. Even at the temperature of absolute zero, 0 K, the electron is in energy level 1. If the electron had zero energy, its location and momentum would be exact. But that is forbidden by the uncertainty principle. There is an equation that is based on the fundamental equation for total energy: E = Ek + Ep Total energy = kinetic energy + potential energy The equation contains the variable, R, for radius, or distance between the electron and the proton. The equation is tested with many values of R. If the result is tidy for a particular radius, that radius is accepted as the radius of an energy level. There is no suitable solution for a radius less than that of energy level 1. Therefore, there is no possibility of the electron's having zero energy, or clinging to the proton at zero distance. A hydrogen atom with its electron at level 1, has a collision of some sort. If the energy which is available from that collision, is less than the energy difference between level 1 and level 2, the electron does not absorb any of that energy. The electron is forbidden to have intermediate energies. The electron must rise from one energy level to another, or not gain energy at all. Photon absorption follows the same rule. A photon is absorbed only if its energy is exactly right for the difference between two energy levels. Other photons can't be absorbed. Forces are negative if they attract, and positive if they repel. The formula for potential energy is: E = Fd E is energy, F is force, d is distance. The potential energy between a proton and an electron is negative. In order to have energy level 5, with more potential energy than energy level 1, level 5 has a small negative number, and level 1 has a large negative number. The potential energy when the electron is completely separated from the proton, is zero. The potential energy when the electron is at level 1, is -2.18 x 10-11 erg. I object to a system in which large is small, and small is large, and energy is negative. The electron at level 1 in the hydrogen atom, has a spherical orbital. The meaning of orbital is not like the meaning of orbit. The orbital is the locus of the most likely points at which the electron might be found. The electron is never at rest. Its location at any instant is uncertain. However it has a definite probability of being in a particular location. The points with the highest probability of containing the electron for an instant, fall on the surface of a sphere. That sphere is the orbital. For level 1, there is a possibility of having an electron in a spherical orbital, with its spin in one direction. It is also possible to have a second electron in the same orbital, with its spin in the opposite direction. For use in calculations, these characteristics of electrons are assigned quantum numbers. There is an n number, which is the same as the level number. The n number could be 1,2,3,4, etc. The l number describes the shape of the orbital. A spherical orbital has an l number of 0. A propeller shaped orbital has l number 1. A negative hydrogen ion is a hyrogen atom with an extra electron. At their least energies, the electrons are in level 1. They have opposite spins. The exclusion principle forbids any two electrons to have all of their quantum numbers in common. Both electrons have n number 1, and l number 0. They are permitted to stay where they are in the same ion, only because they have different spin numbers. The spin number is the s number. One of the electrons has s number +1/2, and the other has s number -1/2. A hydrogen atom in the second energy level has more orbitals. In addition to a spherical orbital, l number 0, there can be an elongated orbital, l number 1. (Fig. 2)

The number 1 shape is like a propeller. A fourth quantum number, the m number orients the orbital. The orbital in (Fig. 3) has m number +1.

The orbital in (Fig. 2) has m number 0. The orbital in (Fig. 4) has m number -1.

Each orientation is perpendicular to the other two orientations. One horizontal orientaion is along the x axis. A second horizontal orientation is along the y axis, ninety degrees from the x axis. The third orientation is vertical, and along the z axis. The orbitals are arrived at by finding solutions to the quantum equation. The equation is difficult to solve for the hydrogen atom. A computer is employed for the purpose. The equation is too hard to solve for the negative hydrogen ion, the hydrogen molecule, or any other atom or molecule. Chemists have found it useful to find approximate solutions, and build their model atoms on that basis. The model of the hydrogen atom is (Fig. 5).

The dot is the proton. The circle is the spherical orbital of the electron. This is the normal state of the hydrogen atom. Add sufficient energy to the hydrogen atom, and it attains an excited state. (Fig. 6)

The electron is on level 2, where it can be either, in a spherical orbital, a, or in a propeller orbital, b. The spherical orbital of level 2 is much larger than the spherical orbital of level 1. The propeller shaped orbital appears on both sides of the nucleus. That does not mean that the electron travels through the proton. It only means that the quantum equation yields a probability of finding the electron on both sides of the proton, not inside the proton. If there is enough energy to promote the electron to level 3, it can be in either, a spherical orbital, a two-bladed propeller orbital, or a four-bladed propeller orbital. (Fig. 7)

Helium, with two electrons, in its normal state, has both electrons on level 1, in the same spherical orbital. Lithium, with 3 electrons, in its normal state, has 2 electrons on level 1, with a spherical orbital. The third electron must go to level 2, because of the exclusion principle. The first two electrons have opposite spins. Therefore they have some small attraction for each other that partially cancels their mutual repulsion. The third electron has the same spin as one of the other electrons. Two electrons with the same spin have an additional weak repulsive force, which combines with the electrostatic repulsive force. The third electron has a large spherical orbital. Beryllium has 4 electrons. The outer 2 electrons are in level 2. One of the outer electrons is in a spherical orbital, called an s orbital. The other outer electron is in a propeller orbital, called a p orbital. Boron has 5 electrons. It is like beryllium, but it has 2 propellers. Carbon, with 6 electrons, has 3 propellers. (Fig. 8)

Neon, with 10 electrons, has the same three propellers. While carbon has only one electron on each of the four orbitals on level 2, neon has 2 electrons on each of the 4 orbitals on level 2. The next element is sodium, with 11 electrons. There is no room left on level 2. There can be no more than 2 electrons per orbital. The first 10 electrons of sodium are accommodated exactly as they are in neon. The eleventh electron of sodium is in level 3 with a spherical orbital of still larger size. The chemical bond is described in terms of orbitals. The atomic orbitals of combining atoms merge to form molecular orbitals. Standard science has no points of zero force. The electrons in a chemical bond wander. They have various probabilities of being in the many points in the vicinity of the molecular bond. Two hydrogen atoms approach each other. Their orbitals extend into the space between atoms. (Fig. 9)

The orbitals overlap as the atoms get closer. The molecular orbital envelops both protons. The protons maintain their distance, because of their mutual repulsion. (Fig. 10)

I want to combine carbon and hydrogen. I see 6 points projecting from the carbon atom. I know that one atom of carbon combines with 4 atoms of hydrogen. There is no compound of formula CH6. Furthermore, I don't expect half an electron to contribute to a bond. When a hydrogen atom comes close to a carbon atom, a propeller alters its shape. (Fig. 11)

Presumably, the shape of the spherical orbital changes when it has an oportunity to participate in a bond. The 4 outer electrons of the carbon atom change the shapes of their orbitals. The resulting orbitals are called hybrid orbitals, or sp3 orbitals. The s stands for one s orbital, and the p3 stands for 3 p orbitals. (Fig. 12)

A proper model of sp3 orbitals is in three dimensions and has an angle of about 109o between orbitals. In some compounds, the carbon atom combines with 3 other atoms. Three orbitals are hybrid orbitals. One orbital remains a p orbital. (Fig. 13)

The hybrid orbitals are called sp2 because there are 2 p orbitals and 1 s orbital. The third p orbital continues to be a p orbital. The sp2 orbitals are all in the same plane, and make an angle of 120o with each other. A complete circle is 360o. A third of a circle is 120o. The plane of the p orbital is perpendicular to the plane of the other 3 orbitals. Hybrid orbitals, like sp2 and sp1 participate in sigma bonds. The double bond between two carbon atoms is a combination of a sigma bond and a pi bond. The unhybridized p orbital participates in the pi bond. (Fig. 14)

The two sets of dots, together, constitute one molecular bond. The other bond of the double bond is the sigma bond. (Fig. 15)

An example of the carbon double bond is ethylene. (Fig. 16)

There is evidence to show that the six atoms of the molecule all lie on the same plane, and the angle between the hydrogen atoms is 120o. The molecular bond theory has some successes, and some failures. It runs into difficulty in the case of the element boron. The boron atom has 5 electrons. Two electrons are in level 1, and three electrons are in level 2. Only the three electrons in level 2 are available for bonding. A possible arrangement is 3 hybrid orbitals with an angle of 120o between them. Each boron atom could then be attached to 3 other boron atoms. (Fig. 17)

All of the atoms would then be on one plane in repeating hexagons. A less likely arrangement is three mutually perpendicular orbitals. In that way a complete boron molecule would consist of 8 boron atoms in the shape of a cube. (Fig. 18)

Neither of these shapes is the shape of the real boron crystal. Every sample of the element boron contains a basic unit in the shape of an icosahedron. (Fig. 19)

The icosahedron has 20 triangular faces and 12 atoms. Of the 36 electrons, 10 have to be outside of the icosahedron to attach it to other icosahedra in a crystal. Only 26 electrons remain to bind the 12 atoms. Each of the 12 atoms is bound to 5 others. The atom has only 2 electrons with which to make 5 connections. In order to rescue the molecular bond theory, somebody suggested a Y shaped bond. (Fig. 20)

The straight lines are ony the outines of a triangle, having no physical significance. The bond is inside the triangle. Every bond must have exactly two electrons. Two of the atoms contribute 1 electron each, for the Y bond. A scheme of contributions appears in (Fig. 21)

The central atom is number zero. Each atom has a number. The numbers inside the triangles identify the sources of the two electrons. Once the crystal is established, one electron is like any other. The electrons lose their identities. I prefer to apply my neg-pos theory and the concept of the point of zero force. I look at the top six atoms of (Fig. 19). This is depicted in (Fig. 22)

I repeat the diagram, omitting the connecting lines. (Fig. 23)

I leave the hindmost atom out of the picture, just to make the drawing simple. I place two electrons near the uppermost atoms. Each electron is represented as a dot. (Fig. 24).

I show lines of attraction between electrons and atoms. (Fig. 25)

GHT=273>

There is a point which is closer to the uppermost atom than to the other five atoms, at which point the pull on the electrons is equal in all directions. That is the point of zero net force. I next turn the figure, so that another atom is uppermost. I find the point of zero force for another pair of electrons. By the same reasoning, I make a symmetrical placement of 2 electrons close to each of the twelve atoms. I had 26 electrons to dispose of. I used 24 electrons. There is a point of zero force in the center of the icosahedron. I place the remaining 2 electrons in the center of the figure. The complete icosahedron becomes bonded to other icosahedra by another set of bonds. I look at three icosahedra. (Fig. 26)

Two electrons are located in the center of the imaginary triangle that joins the imaginary icosahedra. The electrons are at the point of zero force. There are 6 such triangles surrounding the icosahedron. (Fig. 27)

Each triangle contains 2 electrons. My original icosahedon supplied only 4 electrons of the 12. The other 8 electrons came from surrounding icosahedra. The original icosahedron still has 6 electrons to go. The 6 triangles of Fig. 27 are all in the same plane. A glance at Fig. 19 shows that there is a triangular face of the icosahedron in the foreground, which is not on that plane. It is on a parallel plane. The 3 atoms of that triangle have an electron each. I can draw bonds between that triangle and a similar triangle on another icosahedron. I turn the figure, so that the triangle is seen in a new perspective. (Fig. 28)

The drawing is 3 dimensional. Point A is closer to the viewer than side b. I draw the bond lines. (Fig. 29)

The lines connect with the triangle of another icosahedron. (Fig. 30)

There is a background triangle in Fig. 19, which cannot be seen. The situation there is exactly like that of the triangle that can be seen. The six bonds of the front and back triangles are ordinary sigma bonds. Each bond contains 2 electrons and connects 2 atoms. Each icosahedron supplies 1 electron of each of these bonds. Electrons do not have to be directed or instructed to remain with a certain atom, or to move on to another atom. They automatically move away when they are repelled, and approach when they are attracted. They remain in place whenever there are no forces to push them away.