Energy 102
There is an experiment in which a gamma ray interacts with a molecule. The molecule gains a little kinetic energy. The gamma ray is decelerated to a standstill. A negative electron and a positive electron are produced out of the substance of the gamma ray. A gamma ray is a photon with a frequency in the highest known range of frequencies for photons. The frequency of the photon in this experiment is slightly more than 2.48 x 1020 cycle/sec. The energy of a photon of frequency 2.48 x 1020 is 1.64 x 10-6 erg. The neg-pos of the photon with 1.64 x 10-6 erg is 9.6 x 10-10 esu. An electron has 4.8 x 10-10 esu of neg. A positive electron is a positron. A positron has 4.8 x 10-10 esu of pos. The sum of 4.8 x 10-10 and 4.8 x 10-10 is 9.6 x 10-10, the quantity in esu 0f neg-pos for the photon. The potential energy between a widely separated electron-positron pair is 1.64 x 10-6 erg. The electron and the positron share the potential energy equally. The formula for potential energy is E = Fd. E is energy in ergs. F is force in dynes. d is distance in centimeters. When the force is constant, the potential energy is simply the product of F multiplied by d.
The graph of a constant force is a straight line.
|
Fig. 1
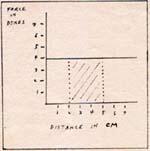To calculate the potential energy change between 2 cm and 5 cm, I produce the vertical dotted lines at 2 cm and 5 cm. I find the area under the horizontal line between 2 cm and 5 cm. The distance between 2 cm and 5 cm is 3 cm. The force represented by the horizontal line is 4 dyne. I multiply 3 cm by 4 dyne and get 12 erg.
Fig. 2
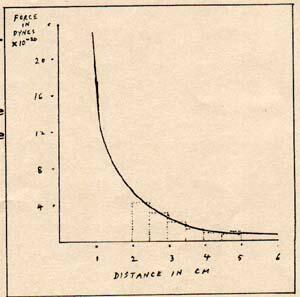The graph of the force between the positron and the electron is a smooth curve. (Fig. 2) The area under the curve between 2cm and 5 cm is easy to find, because the formula for this system is: F = (q1) x (q2) / (d2)
|
For people who are not accustomed to working with such equations, the procedure is to find the areas of a series of rectangles within the dotted lines on fig. 2 The total of the areas is the difference between the potential energy at 5 cm and the potential energy at 2 cm. The answer is approximately 6.9 x 10-20 erg. Assume that the positron and electron have a separation of 5 cm. The attractive force accelerates them equally. As each gains kinetic energy, it loses potential energy. When the separation becomes 2 cm, the electron-positron system has lost 6.9 x 10-20 erg of potential energy and gained 6.9 x 10-20 erg of kinetic energy. When the electron and positron have a separation of zero, they behave like the neg and pos halves of a photon. They radiate neg bits and pos bits in a check pattern. The electron and positron pair turn into a gamma ray photon. If the meeting of the neg and pos takes place in empty space, the neg bits and pos bits pair up and are radiated in two opposite directions, producing two photons. Each of the photons has a frequency of 1.24 x 1020 cycle/sec and neg-pos of 4.8 x 10-10 esu. When the elecrtron and positron meet in the vicinity of a large molecule, the photon is radiated in only one direction , and the molecule absorbs the recoil. The single photon has a frequency of 2.48 x 1020 cycle/sec and neg-pos of 9.6 x 10-10 esu. A proton has mostly neg-pos and a little excess pos. The proton has 8.813 x 10-7 neg-pos and 4.8 x 10-10 pos. The total charge of the proton is 8.818 x 10-7 esu. The proton is a combination of a neg-pos part and a positron part. This is demonstrated in some nuclear reactions which radiate positrons. The attraction between an electron and a proton is fundamentally the attraction between an electron and a positron. The short-range repulsive force of the proton prevents the near approach of the electron to the positron part.
|
Fig. 3
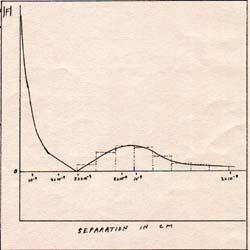The potential energy between a proton and an electron can be calculated from the graph of the force at various distances. (Fig. 3) Another way to find the potential energy of the electron-proton system, when the electron is widely separated from the proton, is to find the highest frequency photon that can be absorbed by a free hydrogen atom.
|
The potential energy of the widely separated electron-proton system is 2.18 x 10-11 erg. That corresponds to 2.66 x 10-15 esu. The potential energy of the electron-proton system, 2.18 x 10-11 erg is is the potential energy of the electron, and will give it motion. The proton feels the same force as the electron, and has 2.18 x 10-11 erg of potential energy, but moves very slightly as it gains kinetic energy, because of its large mass. The electron is accelerated from rest to a kinetic energy of 2.18 x 10-11 erg. On the proton's side, the acceleration is imperceptible, but real.
There is an absolute zero of temperature. A molecule has no translational energy, kinetic energy, oscillation of protons or electrons, or any other than nuclear energy at absolute zero. The absolute temperature scale is called the kelvin scale. One degree of temperature on the kelvin scale is called 1 degree kelvin, and its symbol is 1 K. For 2 degrees kelvin, I write 2 K. The temperature 273 K is the same as 0 C. Translation means moving together as a unit. Each gas molecule has its own translational kinetic energy. For every degree that the temperature rises, the translational kinetic energy of a gas molecule increases by 2.070933 x 10-16 erg. When the translational kinetic energy of a molecule is 6.1713803 x 10-14 erg, the temperature of the molecule is 298 K. Zero on the celsius scale is 273.15 K, but the degree celsius is exactly the same size as the degree kelvin. Room temperature is 298 K, which is 24.85 C.
|
Fig. 4
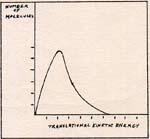A roomful of air at 298 K does not have every molecule at 298 . The great majority are at 298 K, or within a few degrees of 298 K. (Fig. 4) The rest of the molecules have any temperature between 0 and 10,000 K
|
Each molecule has about a billion interactions a second. Therefore the temperature of each molecule changes about a billion times a second. On the other hand, for each billionth of a second, for each millionth of a second, the average tempeature of the molecule doesn't change. Although interactions are so frequent, each interaction upsets the internal order of a molecule. Points of zero force shift, and electrons and protons are put into oscillation. Oscillations are generally referred to as vibrations. The energy of vibration is referred to as vibrational energy. The molecule as a whole is also set into rotary motion. The rotary enegy is referred to as rotational energy. There is an average vibrational energy and rotational energy for each species at each temperature. A hydrogen molecule gains a total of 4.78 x 10-16 erg in rising from 298 K to 299 K . 2.07 x 10-16 erg is translational. The balance, 2.71 x 10-16 erg is a combination of rotational and vibrational. The total of rotational an vibrational is called internal energy. A carbon dioxide molecule gains 6.16 x 10-16 erg in rising from 298 K to 299 K. 2.07 x 10-16 erg is transitional. The rest, 4.09 x 10-16 erg is internal. As a general rule, the more atoms that a gas molecule has, the more internal energy per degree. Hydrogen has two atoms. Carbon dioxide has three atoms. Carbon dioxide has more parts that vibrate. I put a molecule of carbon dioxide into a flask with a molecule of hydrogen. The carbon dioxide starts out with a temperature of 300 K. The hydrogen starts out with a temperature of 290 K. At every interaction some energy is transferred one way or the other. In less than a second, both molecules have the same average temperature. I find the temperature by simple mathematics. The hydrogen molecule gains exactly the amount of energy that the carbon dioxide molecule loses. The energy transfers , on the average, from the molecule that has a higher temperature to the molecule that has a lower temperature. The final temperature is T. The amount of energy that the carbon dioxide yields is (6.16 x 10-16 erg) x (300 - T). 6.16 x 10-16 is the number of ergs yielded per degree. 300 - T is the change in temperature. The amount of energy that the hydrogen gains is (4.78 x 10-16 erg) x (T - 290). 4.78 x 10-16 is the number of ergs per degree that the hydrogen gains. T - 290 is the change in temperature of the hydrogen. The amount yielded equals the amount gained. (6.16 x 10-16) (300 - T) = (4.78 x 10-16) (T - 290) The final temperature is 295.6 K. I have a flask containing a mixture of hydrogen and oxygen. There are twice as many molecules of hydrogen than of oxygen. There is no reaction until I ignite the mixture with a spark or a flame. The reaction doesn't take place until some molecules separate into atoms. It takes a temperature of about 29000 K to give an oxygen molecule enough internal energy, 8.2 x 10-12 erg, to separate the atoms. In the presence of free hydrogen atoms, the oxygen molecule can be broken at a lower temperature. There remains the difficulty that it takes a temperature of about 26000 K to give a hydrogen molecule 7.1 x 10-12 erg of internal energy to break the bond. The temperature of a match flame is about 2000 K. The average translational kinetic energy of a molecule at 2000 K is 4.14 x 10-13 erg. That is 1/17 the required enegy. There are a few energetic molecules at 2000 K , and some of them can supply 7.1 x 10-12 erg. By using a match flame, I convert some hydrogen molecules into hydrogen atoms. The reaction is: H-H -----> H + H This is pictured in Fig. 5.
|
Fig. 5
1. A fast-moving molecule arrives from the left, and pushes the left side of the hydrogen molecule. 2. The protons get pushed close, where they repel strongly.
3. The atoms are repelled in opposite directions. As the atoms separate, they decelerate, because they still attract each other. The kinetic energy of 7.1 x 10-12 erg is changed into potential energy, when the atoms are far apart.
|
It is unlikely that both hydrogen atoms arrive at an oxygen molecule at the same instant. One hydrogen atom arrives at an oxygen molecule. The reaction is: H + O=O -----> H-O-O This is pictured in Fig. 6.
|
Fig. 6
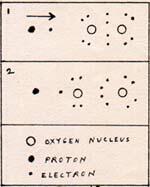
1. A free hydrogen atom approaches an oxygen molecule. The hydrogen electron is attracted to an oxygen nucleus, which is incompletely surrounded by electrons.
2. The oxygen electrons rearrange themselves, making room for the incoming electron. The resulting molecule is somewhat unstable.
|
The strength of the oxygen molecule is in its, so called, double bond. A bond is our way of thinking about the forces that hold a molecule together. The double bond is an array of four electrons between two atoms. The arrival of the new electron pushes the other electrons to the right, disrupting the double bond. Therefore the molecule is slightly unstable. The breaking of one bond of a double bond of oxygen takes less than half of the energy of the double bond. The arriving hydrogen atom has very little kinetic energy, but relative to oxygen, the hydrogen atom has more potential energy than its potential energy toward another hydrogen atom. The hydrogen atom accelerates toward the oxygen, and arrives with a kinetic energy equal to the potential energy of its attraction. The kinetic energy is at a maximum at the point of zero net force for the hydrogen atom, at which point the potential energy is zero. The point of zero net force for the hydrogen atom is really two points, one for the proton, one for the electron. Every point of zero force in the oxygen molecule has to shift. That sets up oscillation in all parts, at the expense of some of the kinetic energy of the hydrogen atom. The distance between oxygen nuclei increases, because the addition of one electron increases the repulsion among the outer electrons, forcing them to yield and spread out a little. A hydrogen molecule arrives at the H-O-O molecule. The reaction is: H-H + H-O-O -----> H-O-H + O-H This is pictured in Fig. 7.
|
Fig. 7
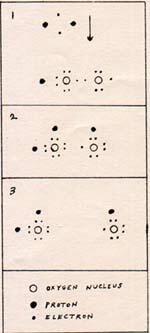
1. A hydrogen molecule approaches a H-O-O molecule.
2. The electrons of the hydrogen molecule find room in the outer layer of the oxygen atoms. There is no bond left between the hydrogen atoms.
3. The electrons are overcrowded. This forces the oxygen atoms to separate.
|
The separation of the two hydrogen atoms and their joining the H-O-O molecule is one single act. The attraction of oxygen for hydrogen is 14% greater than the attraction of hydrogen for hydrogen. Therefore, hydrogen atoms arrive at the oxygen with considerable kinetic energy, with enough left over to separate the oxygen atoms. One of the products is H-O-H, water, which is too stable to react. There remains a H-O molecule. A hydrogen atom arrives at the H-O molecule. The reaction is: H-H + H-O -----> H-O-H + H This is pictured in Fig. 8.
|
Fig. 8
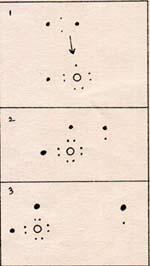
1. A hydrogen molecule approaches the H-O molecule.
2. One hydrogen electron is attracted to the incompletely covered oxygen nucleus. The other hydrogen atom loses its bond.
3. The free hydrogen atom departs. A water molecule remains.
|
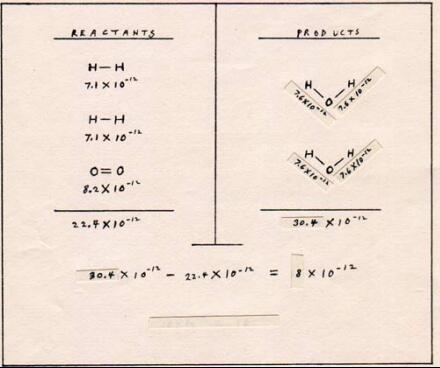
So far, a free hydrogen atom and two water molecules have resulted from the combination of one oxygen molecule , two hydrogen molecules, and a free hydrogen atom. That free hydrogen atom can start another cycle of production of two water molecules. That is a chain reaction , but it can stop abruptly if the free hydrogen atom joins something other than an oxygen molecule. At every step, the oscillations of the atoms increase. This raises the temperature of the mixture of gases. Therefore there are more molecules with exceptionally high temperatures . They produce more free hydrogen atoms without the help of any more sparks or match flames. The temperature rises because the translational kinetic energy increases. The translational kinetic energy increases because molecules that have increased oscillation, transfer some of their internal kinetic energy to other molecules in collisions. Often internal kinetic energy in one molecule becomes translational kinetic energy in another molecule. The reverse can also happen,but, on the average, energy passes from the molecule with the higher temperature to the molecule with the lower temperature. By way of analogy, if I run toward a soccer ball that is in the air, and I hit it with my chest, it gains less motion than if I take a running leap and kick the ball at the same time. That kick is the internal energy. In a molecule it is an atom during the outward directed portion of a vibration. The rise in temperature is so fast, that the conversion of 2.55 x 1022 molecules of oxygen and 5.1 x 1022 molecules of hydrogen into 5.1 x 1022 molecules of water vapor takes a small fraction of a second. It is an explosion. The source of the energy in this reaction is in the potential energy between hydrogen atoms and oxygen atoms. As I describe this reaction, no energy has come from outside or gone to the outside. The only thing that changes is the temperature. I permit my product, the 5.1 x 1022 molecules of water vapor, to have contact with the air in the room. The final temperaature is 298 K. In changing from a gas at a high temperature of 6733 K to a liquid at 298 K, the 5.1 x 10 22 molecules of water yield 2.55 x 1011 erg. That amounts to 5 x 10-12 erg per molecule. The accounting of the energy that goes into breaking bonds, and the energy that is yielded in making bonds, helps to illustrate what happens to energy in a chemical reaction. Fig. 9 is a chart of such an account.
|
Fig. 9
|
The energy of the reaction is 8 x 10-12 erg when two molecules of hydrogen combine with one molecule of oxygen. Counting the double bond of oxygen as one bond, there are three bonds among the reactants and four bonds among the products. The extra bond in the products column accounts for much of the energy that becomes available to the surroundings.
|